A rectifier is an electrical device that converts alternating current (AC) to direct current (DC), a process known as rectification. This almost always involves the use of some device that only allows one-way flow of electrons, a diode. Below schematic diagram shows a Three-Phase Full Wave Bridge Rectifier Circuit Diagram. Each three-phase line connects between a pair of diodes: one to route power to the positive (+) side of the load, and the other to route power to the negative (-) side of the load.
Labels
- 2.1 Channel Systems (1)
- 6C45Pi (2)
- Active Filter (4)
- alarm systems (2)
- Amplifier (9)
- Amplifier Class G (2)
- Audio - Alarm (1)
- Audio Circuits (1)
- Audio Processor (1)
- Basic Electronics (5)
- Build Speaker (1)
- Car Audio (1)
- Ceramic Speaker (1)
- Charger (1)
- Circuits (2)
- Class A (2)
- DIY Speaker Cables (2)
- DIY Speakers (1)
- Electronic Circuit (1)
- Electronics (2)
- FM Transmitter (6)
- LA47536 (1)
- LF353 (1)
- LM1558 (1)
- LM358 (1)
- LM3886 (1)
- Modding (1)
- NE5532 (1)
- Oscillator (4)
- Others (18)
- Power Amplifier (20)
- Power Meter (1)
- Power RF (1)
- Power Supply (2)
- Protection Circuit (1)
- Radio (1)
- Rectifiers (4)
- RF Measurement (1)
- Schematics (2)
- Single Ended (2)
- Speaker Cables (2)
- Speakers (1)
- Subwoofer (2)
- SWR Meter (1)
- SWR Protection Circuit (2)
- TDA1517 (1)
- TDA7240 (1)
- TIP33 (1)
- TIP34 (1)
- Tone control - Graphic Equaliser (1)
- Transformer (1)
- Transistor (4)
- usb wifi antenna (5)
- Voltage Multipliers (1)
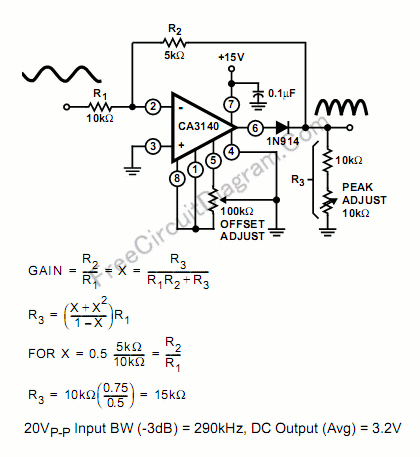
Single Supply Precise Full Wave Rectifier Using CA3140 Op-Amp
The schematic diagram below describe a precise full-wave rectifier circuit. The circuit needs only a single supply, make it suitable for battery operated devices.
During the positive cycle of the input, the signal is directly fed through the feedback network to the output, give the transfer function of Vout=R3/(R1+R2+R3). At the positive cycle of the input, the diode 1N914 disconnect the op-amp output because the op-amp output is zeroed.
During a negative cycle of the input signal, the CA3140 functions as a normal inverting amplifier with a gain equal to -R2/R1. When the equality of the two equations shown in the Figure is satisfied, the full wave output is symmetrical. Note that the output is not buffered, so the output should be connected only to high impedance stage, with impedance much higher than R3. Errata: the figure shows an equation of GAIN=(R2/R1)=X=(R3/(R1R2+R3)) that is wrong, and the right formula should be GAIN=(R2/R1)=X=(R3/(R1+R2+R3)). [Circuit's schematic diagram source: Intersil Application Notes]
Greatly Expanded Scale Circuit Using LM3914

Placing the LM3914 internal resistor divider in parallel with a section (230Ω) of a stable, low resistance divider greatly reduces voltage changes due to IC resistor value changes with temperature. Voltage V1 should be trimmed to 1.1V first by use of R2. Then the voltage V2 across the IC divider string can be adjusted to 200mV, using R5 without affecting V1. LED current will be approximately 10mA. [Schematic source: National Semiconductor, Inc].
Swimming Pool Solar Heat Control Circuit

A thermistor with a resistance of about 100 kΩ at 25°C should be selected. One such thermistor is the ACW-027 from Ketema, which can be clamped around a pipe in the solar panel. This circuit will energize the pump when the sun is heating the panels and turn off the pump when the sky is cloudy or the sun goes down. To prevent rapid cycling of the pump during partly cloudy conditions, the hysteresis is set for a relatively wide (20°F) span. Providing low thermal impedance between the thermistor assembly and the solar panel will also prevent rapid pump cycling by adding the solar panel’s thermal time constant to the hysteresis. To select the set point resistors, consult the thermistor data sheet for the thermistor’s value at the desired temperature. For example, assume that we want the pump to turn on (high set point) at 100°F and turn off (low set point) at 80°F. [Schematic diagram source: Microchip Technology, Inc].
Negative Resistance Oscillator Circuits

In this circuit, a negative resistance configuration is used to generate the sine wave. The Q1-Q2 pair provides a 15 μA current source. Q2's collector current sets Q3's peak collector current. The 300 kΩ resistor and the Q4-Q5 LM394 matched pair accomplish a voltage-to-current conversion that decreases Q3's base current when its collector voltage rises. This negative resistance characteristic permits oscillation. The frequency of operation is determined by the LC in the Q3-Q5 collector line. The LF353 FET amplifier provides gain and buffering. Power supply dependence is eliminated by the zener diode and the LF353 unity gain follower. This circuit starts quickly and distortion is inside 1.5%.
Stepper Motor Controller

LMC555 CMOS timer integrated circuit (IC1) generates 200 microsecond pulses to step the motor and control its speed. The speed of the motor can be changed by changing the frequency of this pulse, R1 variable resistor is provided for this purpose. At the output of IC1 (pin 3), a negative going clock pulse drive the gate of IRL530N (Q1) power FET that momentarily turns OFF and disconnects the driver board from ground. This power interruption sends a signal to the motor driver to step the motor. The rotation direction is controlled by the polarity of the voltage applied to the driver circuit through interconnect lines L1 and L2. MPSA05 Bipolar NPN transistor Q2 and MPSA55 PNP transistors Q3 and Q4 invert the pulse from pin 3, pull the drain of Q1 UP when it is OFF. Toggle switch S1 sets its direction by switching polarity. Pushbutton S2 starts and stops the motor by turning the clock on and off.
Parts
C1 – .47 MFD 35 volt tantalum
C2 – 1000 MFD 35 volt electrolytic
C3 – .1 MFD 50 volt metalized film
C4 – .001 MFD 50 volt metalized film
C5 – 100 MFD 16 volt electrolytic
R1 – 5MEG potentiometer
R2, R8, R10 – 100K 1/8 watt 5%
R3 – .56K 1/8 watt 5%
R4, R5, R7 – 10K 1/8 watt 5%
R6 – 2K 1/8 watt 5%
R9 – 4.7K 1/8 watt 5%
Q1 – MPSA05 NPN transistor
Q2, Q3 – MPSA55 PNP transistor
Q4, Q5, Q6, Q7, Q8 – IRL530N Hexfet
D1, D2, D3 – 1N914 silicon diode
D4, D5 – 1N4752 zener diode
D6 – 1N4004 rectifier
BR1 - 2 AMP 400 volt bridge rectifier
IC1 – LMC555 CMOS timer
IC2, IC5 – 78L05 5 volt regulator
IC3 – CD4013 dual D flip flop
IC4 – CD4070 quad exclusive or
S1 – momentary N/O push button switch
S2 – double pole double throw toggle switch
T1 – DC or AC adapter transformer to match motor
IC socket – 1 eight pin
IC sockets – 2 fourteen pin
Terminal blocks – 2 two position
M1, M2 – two phase unipolar 24 volts
Transformer Voltage Booster Circuit: DC-DC Step-Up Switching Regulator Using Transistors

The most interesting this is that circuits use a discrete component: no integrated chip is required, only few transistors with few passive components. Because the switching topology is a boost converter, this circuit cannot be operated as step-down regulator, so the output will always be higher than the input. The voltage output is depend on the load because the feedback mechanism, through the zener diode, will maintain the output at about 14 volt, regardless the voltage input variation and load current variation. The current from the voltage divider will flow through the zener diode if the output goes higher than the nominal value, and this condition will stop the oscillator built around the 2N3904 transistors. Stopping the oscillator will drop the output voltage and thus maintain the required voltage level at the output. This transistor (Q1, Q2, and Q3) form a Schmidt trigger that drive the final transistor Q4 (the switching transistor 2N3053).
This circuit is suitable for battery booster, if you need to run your 12 volt equipments on your old car that is provide only a 6V supply from the battery. The output of this voltage double can be adjusted by changing the voltage divider, or for easier adjustment, you can replace the 4,7K resistor with a 5K potentiometer. Using a good inductor (low resistance), you can achieve up to 80% efficiency, and up to 2 Watt power can be delivered to the load. [Circuit's schematic diagram source: Bill Bowden's circuit collection]
Precision Relaxation Oscillator Circuit Using LM131

The general description about this circuit is the circuit is a feedback loop that keeps this capacitor charged to a voltage very slightly higher than the input voltage, VIN. If VIN is high, CL discharges relatively quickly through RL, and the circuit generates a high frequency. If Vin is low, CL discharge slowly, and the converter puts out a low frequency. When CL discharges to a voltage equal to the input, the comparator triggers the one-shot. The one-shot closes the current switch and also turns on the output transistor. With the switch closed, current from the current source recharges CL to a voltage somewhat higher than the input. Charging continues for a period determined by RT and CT. At the end of this period, the one-shot returns to its quiescent state and CL resumes discharging. [Schematic’s source: National Semiconductor, Inc].
Battery Charger Circuit Using Ammeter VU

The circuit is nothing but a 12V DC power supply with an ammeter for monitoring the charging current. The two diodes forms a centre tapped full wave rectifier. The capacitor filters the rectifier output to produce a clean 12V out put. At initial stages of charging the ammeter will read about 1 to 3 amperes. As the battery is slowly charged the current slowly decreases. For indicate when the battery is fully charged, the ammeter reading will be zero. For attention, it is always be careful to connect the charger to the battery in correct polarity. The polarity is connecting between positive to positive and negative to negative.
Op-Amps with negative feedback
Op-Amps with negative feedback
– There are several basic ways in which an op-amp can be connected using negative feedback to stabilize the gain and increase frequency response.
– The large open-loop gain of an op-amp creates instability because a small noise voltage on the input can be amplified to a point where the amplifier is driven out of the linear region.
– Open-loop gain varies between devices.
– Closed-loop gain is independent of the open-loop gain.
Closed-Loop voltage gain, Acl
– It is the voltage gain of an op-amp with external feedback.
– Gain is controlled by external components.
Noninverting Amplifier
– The op-amp circuit shown below is a non-inverting amplifier in a closed-loop configuration.
– Input signal is applied to the non-inverting input.
– The output is applied back to the inverting input through feedback (closed loop) circuit formed by the input resistor Ri and the feedback resistor Rf.
– This creates a negative feedback.
– The two resistors create a voltage divider, which reduces Vout and connects the reduced voltage Vf to the inverting input.
– The feedback voltage is:
Vf = Ri/(Ri + Rf)Vout
– The difference between the input voltage and the feedback voltage is the differential input to the op-amp.
– This differential voltage is amplified by the open loop gain, Aol, to get Vout.
Vout = Aol(Vin – Vf)
– Let B = Ri/(Ri + Rf). Thus Vf = BVout and
Vout = Aol(Vin – BVout)
– Manipulate the expression to get:
Vout = AolVin - AolBVout
Vout + AolBVout = AolVin
Vout(1 + AolB) = AolVin
Overall Gain = Vout/Vin = Aol/(1 + AolB)
– Since AolB >> 1, the equation above becomes:
Vout/Vin = Aol/(AolB) = 1/B
– Thus the closed loop gain of the noninverting (NI) amplifier is the reciprocal of the attenuation (B) of the feedback circuit (voltage-divider).
Acl(NI) = Vout/Vin = 1/B = (Ri + Rf)/Ri
– Finally:
Acl(NI) = 1 + Rf/Ri
– Notice that the closed loop gain is independent of the open-loop gain.
Example
Determine the gain of the amplifier circuit shown below. The open loop gain of the op-amp is 150000.
Solution
This is a noninverting amplifier op-amp configuration. Therefore, the closed-loop voltage gain is
Acl(NI) = 1 + Rf/Ri = 1 + 100 k?/4.7 k? = 22.3
Voltage-Follower (VF)
– Output voltage of a noninverting amplifier is fed back to the inverting input by a straight connection.
– The straight feedback has a gain of 1 (i.e. there is no gain).
– The closed-loop voltage gain is 1/B, but B = 1. Thus, the Acl(VF) = 1.
– It has very high input impedance and low output impedance.
Inverting Amplifier (I)
– The input signal is applied through a series input resistor Ri to the inverting input.
– The output is fed back through Rf to the same input.
– The noninverting input is grounded.
– For finding the gain, let’s assume there is infinite impedance at the input (i.e. between the inverting and non-inverting inputs).
– Infinite input impedance implies zero current at the inverting input.
– If there is zero current through the input impedance, there is NO voltage drop between the inverting and noninverting inputs.
– Thus, the voltage at the inverting input is zero!
- The zero at the inverting input is referred to as virtual ground.
– Since there is no current at the inverting input, the current through Ri and the current through Rf are equal:
Iin = If.
– The voltage across Ri equals Vin because of virtual ground on the other side of the resistor. Therefore we have that
Iin = Vin/Ri.
– Also, the voltage across Rf equals –Vout, because of virtual ground. Therefore:
If = -Vout/Rf
– Since If = Iin, we get that:
-Vout/Rf = Vin/Ri
– Or, rearranging,
Vout/Vin = -Rf/Ri
– So,
Acl(I) = -Rf/Ri
– Thus, the closed loop gain is independent of the op-amp’s internal open-loop gain.
– The negative feedback stabilizes the voltage gain.
– The negative sign indicates inversion.
Full-wave rectifiers
Full-wave rectifiers
– Half-wave rectifiers have some applications.
– However, full-wave rectifiers are the most commonly used ones for dc power supplies.
– A full-wave rectifier is exactly the same as the half-wave, but allows unidirectional current through the load during the entire sinusoidal cycle (as opposed to only half the cycle in the half-wave).
– Average value of output becomes twice that of the half wave rectifier output:
VAVG = 2Vp/p
– There are two main types of full wave rectifiers:
i) Center-tapped full-wave rectifier.
– Two diodes connected to the secondary of a center-tapped transformer.
– Half of Vin shows up between the center tap and each secondary.
– At any point in time, only one of the diodes is forward biased.
– This allows for continuous conduction through load.
– Note that the peak inverse voltage (PIV) across D2 is:
PIV = (Vp(sec)/2 – 0.7) – (-Vp(sec)/2)
= (Vp(sec)/2 + Vp(sec)/2 – 0.7)
= Vp(sec) – 0.7
– Since Vp(out) = Vp(sec)/2 – 0.7, we get:
Vp(sec) = 2Vp(out) + 1.4
– Thus, the PIV across each diode becomes:
PIV = 2Vp(out) + 0.7 V
ii) Bridge full-wave rectifier.
– When the input cycle is positive, diodes D1 and D2 are forward biased.
– When the input cycle is negative, diodes D3 and D4 are the ones conducing.
– The output voltage becomes:
Vp(out) = Vp(sec) – 1.4 V
– The reason we’d rather use a full bridge rectifier than a center-tap, is that the PIV is a lot smaller:
PIV = Vp(out) + 0.7 V
The Transistor as an Amplifier
The Transistor as an Amplifier
– Amplification is the process of linearly increasing the amplitude of an electrical signal.
– A transistor can act as an amplifier directly using the gain, b.
– Keep in mind that when a transistor is biased in the active (linear) region, the BE junction has a low resistance due to forward bias and the BC junction has a high resistance due to reverse bias.
i) DC and AC quantities
– Amplifier circuits have both ac and dc quantities.
– Capital letters are used will be used for both ac and dc currents.
– Subscript will be capital for dc quantities.
– Subscript will be lowercase for ac quantities.
ii) Transistor amplification
– A transistor amplifies current because the collector current is equal to the base current multiplied by the current gain, b.
– Base current (IB) is small compared to IC and IE.
– Thus, IC is almost equal to IE.
– Consider the following circuit.
– An ac voltage, Vin, is superimposed on the dc bias voltage VBB.
– DC bias voltage VCC is connected to the collector through the collector resistance, RC.
– The ac input voltage produces an ac base current, which results in a much larger ac collector current.

– The ac collector current produces an ac voltage across RC, thus producing an amplified, but inverted, reproduction of the ac input voltage in the active region.
– The forward biased base-emitter junction present low resistance to the ac wave.
– This internal ac emitter resistance is designated r’e.
Ie ? Ic = Vb/ r’e
– The ac collector voltage, Vc = IcRC.
– Since Ie ? Ic, the ac collector voltage is Vc ? IeRC.
– Vb can be considered the transistor ac input voltage where Vb = Vin – IbRB.
– Vc can be considered the transistor ac output voltage.
– The ratio of Vc to Vb is the ac voltage gain, Av, of the transistor circuit.
Av = Vc/Vb
– Substituting IeRC for Vc and Ie r’e for Vb yields
Av = Vc/Vb ? (IeRC)/(Ie r’e) = RC/ r’e
– Thus, amplification depends on the ratio of RC and r’e.
– RC is always considerably larger in value than r’e, thus the output voltage is larger than the input voltage.
Example:
Determine the voltage gain and the ac output voltage for the following circuit if r’e = 50 W.
Solution:
The voltage gain is
Av ? RC/r’e = 1 k W /50 W = 20
Thus the output voltage is
Vout = AvVb = (20)(100 mV) = 2 Vrms
Op-Amp Input Modes and Parameters
Op-Amp Input Modes and Parameters
– There are several input modes for an op-amp.
i) Single-Ended Input.
– One input is grounded and the input voltage is applied to the other.
– If the voltage is applied to the inverting input, an inverted amplified signal is seen at the output.
– A non-inverted amplified signal is seen if the input voltage is applied to the non-inverting input.
ii) Differential input.
– Two opposite polarity (out-of-phase) signals are applied to the inputs.
– The amplified difference between the two inputs appears on the output.
iii) Common-Mode Input.
– Two signal voltages of the same phase, frequency, and amplitude are applied to the two inputs.
– They should cancel out to yield an output equal to zero.
– This is called the common-mode rejection.
– Its importance lies in the situation where an unwanted signal appears commonly on both op-amp inputs.
– The unwanted signal will not appear at the output.
– Thus, only the desired signal will show up at Vout.
Common-Mode Rejection Ratio (CMRR)
– This is the measure of an amplifier’s ability to reject common-mode signals.
– Ideally, complete rejection of common signals should be seen.
– However, there is some small common-mode gain (much less than 1).
– The higher the open-loop gain with respect to the common-mode gain, the better the performance of the op-amp (in terms of rejecting unwanted signals).
– Thus, the ratio between the open-loop voltage gain and the common-mode gain becomes:
CMRR = Aol/Acm
– The higher the CMRR, the better.
– We may also express it in decibels (dB):
CMRR = 20 log(Aol/Acm)
– The open-loop voltage gain (also called the large-signal voltage gain) is the gain of the device when there are no external components.
– It may be up to 200000 and it is not a well controlled parameter.
– A CMRR of 100000 means that the desired input signal (differential) is amplified 100000 times more than the unwanted noise (common-mode).
Common-Mode Input Voltage Range
– Range of input voltages which, when applied to both inputs, will not cause clipping or other output distortion.
– Typical values ±10 V with dc supply voltage of ±10 V.
Input Offset Voltage (VOS)
– Ideally, zero volts out for zero volts in.
– In practice, a small dc voltage, VOUT(error), appears at the output with no differential input voltage applied.
– Typical values are between 2 mV or less.
Input Offset Voltage Drift with Temperature
– How much change there is in the input offset voltage for each degree of change in temperature.
– Typical values are between 5 ?V/oC to 50 ?V/oC.
Input-Bias Current
– Input bias current is the dc current required by the inputs of the amplifier to properly operate it.
– The input bias current is the average of both input currents:
IBIAS = (I1 + I2)/2
Input Offset-Current
– Ideally, it is zero, since it is the difference between the two input currents.
– In practice:
IOS = |I1 - I2|
– This could become a problem if both dc input currents are not the same.
Slew Rate
– Maximum rate of change of output voltage in response to a step input.
Full-wave rectifiers definition and explanation
Full-wave rectifiers
– Half-wave rectifiers have some applications.
– However, full-wave rectifiers are the most commonly used ones for dc power supplies.
– A full-wave rectifier is exactly the same as the half-wave, but allows unidirectional current through the load during the entire sinusoidal cycle (as opposed to only half the cycle in the half-wave).
– Average value of output becomes twice that of the half wave rectifier output:
VAVG = 2Vp/p
– There are two main types of full wave rectifiers:
i) Center-tapped full-wave rectifier.
– Two diodes connected to the secondary of a center-tapped transformer.
– Half of Vin shows up between the center tap and each secondary.
– At any point in time, only one of the diodes is forward biased.
– This allows for continuous conduction through load.
– Note that the peak inverse voltage (PIV) across D2 is:
PIV = (Vp(sec)/2 – 0.7) – (-Vp(sec)/2)
= (Vp(sec)/2 + Vp(sec)/2 – 0.7)
= Vp(sec) – 0.7
– Since Vp(out) = Vp(sec)/2 – 0.7, we get:
Vp(sec) = 2Vp(out) + 1.4
– Thus, the PIV across each diode becomes:
PIV = 2Vp(out) + 0.7 V
ii) Bridge full-wave rectifier.
– When the input cycle is positive, diodes D1 and D2 are forward biased.
– When the input cycle is negative, diodes D3 and D4 are the ones conducing.
– The output voltage becomes:
Vp(out) = Vp(sec) – 1.4 V
– The reason we’d rather use a full bridge rectifier than a center-tap, is that the PIV is a lot smaller:
PIV = Vp(out) + 0.7 V
SWR Protection Circuit
Transistor Characteristics
Transistor Characteristics and Parameters
– The ratio of the dc collector current (IC) to the dc base current (IB) is the dc beta (bDC).
– bDC is called the gain of a transistor:
bDC = IC/IB
– Typical values of bDC range from less than 20 to 200 or higher.
– bDC is usually designated as an equivalent hybrid (h) parameter:
hFE = bDC
– The ratio of the collector current (IC) to the dc emitter current (IE) is the dc alpha (aDC). This is a less-used parameter than beta.
aDC = IC/IE
– Typical values range from 0.95 to 0.99 or greater.
– aDC is always less than 1.
– This is because IC is always slightly less than IE by the amount of IB.
– From graph above we can see that there are 6 important parameters to be considered:
i) IB: dc base current.
ii) IE: dc emitter current.
iii) IC: dc collector current.
iv) VBE: dc voltage at base with respect to emitter.
v) VCB: dc voltage at collector with respect to base.
vi) VCE: dc voltage at collector with respect to emitter.
– VBB forward-biases the BE junction.
– VCC reverse-biases the BC junction.
– When the BE junction is forward biased, it is like a forward biased diode:
VBE ? 0.7 V
– But it can be as high as 0.9 V (and is dependent on current). We will use 0.7 V from now on.
– Emitter is at ground. Thus the voltage across RB is
VR(B) = VBB- VBE
– Also
VR(B) = IRRB
– Or:
IRRB = VBB- VBE
– Solving:
IB = (VBB- VBE)/RB
– Voltage at collector with respect to grounded emitter is:
VCE = VCC – VR(C)
– Since drop across RC is VR(C) = ICRC the voltage at the collector is also:
VCE = VCC - ICRC
– Where IC = bDCIB. Voltage across the reverse-biased collector-bias junction is
VCB = VCE - VBE
Example:
Determine IB, IC, IE, VBE, VCE, and VCB in the following circuit. The transistor has bDC 150.
Solution:
We know VBE=0.7 V. Using the already known equations:
IB = (VBB- VBE)/RB
IB = (5 – 0.7)/10kW = 430 mA
IC = bDCIB = (150)( 430 mA) = 64.5 mA
IE = IC + IB = 64.5 mA + 430 mA = 64.9 mA
Solving for VCE and VCB:
VCE = VCC – ICRC = 10V-(64.5mA)(100W) = 3.55 V
VCB = VCE – VBE = 3.55 V – 0.7 V = 2.85 V
Since the collector is at higher potential than the base, the collector-base junction is reverse-biased.
– Changing the voltage supplies with variable voltage supplies in the circuit above, we can get the characteristic curves of the BJT.
– If we start at some positive VBB and VCC = 0 V, the BE junction and the BC junction are forward biased.
– In this case the base current is through the BE junction because of the low impedance path to ground, thus IC is zero.
– When both junctions are forward-biased, the transistor is in the saturation region of operation.
– As VCC is increase, VCE gradually increases, as the IC increases (This is the steep slope linear region before the small-slope region).
– IC increases as VCC increase because VCE remains less than 0.7 V due to the forward-biased base-collector junction.
– Ideally, when VCE exceeds 0.7 V, the BC junction becomes reverse biased.
– Then, the transistor goes into the linear region of operation.
– When the BC junction is reverse-biased, IC levels off and remains essentially constant for a given value of IB as VCE continues to increase.
– Actually, there is a slight increase in IC, due to the widening of the BC collector depletion region, which results in fewer holes for recombination in the base, which causes a slight increase in bDC.
– For the linear portion, the value of IC is calculated by:
IC = bDCIB
– When VCE reaches a sufficiently large voltage, the reverse biased BC junction goes into breakdown.
– Thus, the collector current increases rapidly.
– A transistor should never be operated in this region.
– When IB = 0, the transistor is in the cutoff region, although there is a small collector leakage current.
i) Cutoff
– As said before, when IB = 0, transistor is in cutoff region.
– There is a small collector leakage current, ICEO.
– Normally it is neglected so that VCE = VCC.
– In cutoff, both the base-emitter and the base-collector junctions are reverse-biased.
ii) Saturation
– When BE junction becomes forward biased and the base current is increased, IC also increase (IC – bDCIB) and VCE decreases as a result of more drop across the collector resistor (VCE = VCC – ICRC).
– When VCE reaches its saturation value, VCE(sat), the BC junction becomes forward-biased and IC can increase no further even with a continued increase in IB.
– At the point of saturation, IC = bDCIB is no longer valid.
– VCE(sat) for a transistor occurs somewhere below the knee of the collector curves.
– It is usually only a few tenths of a volt for silicon transistors.
iii) DC load line
– Cutoff and saturation can be illustrated by the use of a load line.
– Bottom of load line is at ideal cutoff (IC = 0 and VCE = VCC).
– Top of load line is at saturation (IC = IC(sat) and VCE = VCE(sat))
– In between cutoff and saturation along the load line is the active region.
– More to come later.
Example
Determine whether or not the transistor in circuit below is in saturation. Assume VCE(sat) = 0.2 V.
First determine IC(sat).
IC(sat) = (VCC – VCE(sat))/RC
IC(sat) =(10 V – 0.2V)/10kW = 9.8 mA
Now let’s determine whether IB is large enough to produce IC(sat).
IB = (VBB - VBE)/RB = (3 V – 0.7 V)/10kW = 0.23 mA
IC = bDCIB = (50)(0.23 mA) = 11.5 mA
This shows that with the specified bDC, this base current is capable of producing an IC greater than IC(sat). Thus, the transistor is saturated, and the collector current value of 11.5 mA is never reached. If you further increase IB, the collector current remains at its saturation value.
i) More on bDC
– The bDC of hFE is not truly constant.
– It varies with collector current and with temperature.
– Keeping the junction temperature constant and increasing IC causes bDC to increase to a maximum.
– Further increase in IC beyond this point causes bDC to decrease.
– If IC is held constant and temperature varies, bDC changes directly with temperature.
– Transistor data specify bDC at specific values. Normally the bDC specified is the maximum value.
ii) Maximum transistor ratings
– Maximum ratings are given for collector-to-base voltage, collector-to-emitter voltage, emitter-to-base voltage, collector current, and power dissipation.
– The product VCEIC must not exceed PD(max).
Example:
The transistor shown in the figure below has the following maximum ratings: PD(max)=800 mW, VCE(max) = 15 V, and IC(max) = 100 mA. Determine the maximum value to which VCC can be adjusted without exceeding a rating. Which rating would be exceeded first?
Solution:
First, find IB, so that you can determine IC.
IB = (VBB – VBE)/RB = (5 V – 0.7 V)/22 kW = 195 mA
IC = bDCIB = (100)(195 mA) = 19.5 mA
IC is much less than IC(max) and will not change with VCC. It is determined only by IB and bDC.
The voltage drop across RC is
VR(C) =ICRC = (19.5 mA)(1 kW) = 19.5 V
Now we can determine the value of VCC when VCE = VCE(max) = 15 V.
VR(C) = VCC - VCE
So,
VCC(max) = VCE(max) + VR(C) = 15 V + 19.5V = 34.5 V
VCC can be increased to 34.5 V, under the existing conditions, before VCE(max) is exceeded. However, at this point it is not known whether or not PD(max) has been exceeded:
PD = VCE(max)IC = (15 V)(19.5 mA) = 293 mW
Since PD(max) is 800 mW, it is not exceeded when VCC = 34.5 V. So, VCE(max) = 15 V is the limiting rating in this case. If the base current is removed, causing the transistor to turn off, VCE(max) will be exceeded first because the entire supply voltage, VCC, will be dropped across the transistor.




August 31st, 2009 at 4:19 pm
the article proved extremely useful in clearing my concept especially regarding saturation region